Answer:
The required equation is y = 3x + 17. Correct: B)
Step-by-step explanation:
Equation of a line
A line can be represented by an equation of the form
y=mx+b
Where x is the independent variable, m is the slope of the line, m is the y-intercept and y is the dependent variable.
We are given the equation of a line as (corrected)
y=-1/3x+2
Note the slope of this line is m1=-1/3
We are asked to find the equation of another line that is perpendicular to the one above. Two lines are perpendicular if their slopes comply with the following condition:
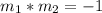
Since we have m1, find m2:
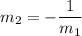
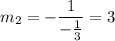
This means the slope of the required line is 3. We only have to test the options to find which one of us contains the point (-5,2):
A) The slope of this line is 3, so we test the point (-5,2)
2=3(-5)+13=-15+13=-2
Since 2 is different from -2, this option is not correct
B) The slope of this line is 3, so we test the point (-5,2)
2=3(-5)+17=-15+17=2
Since equality stands, this is the correct option
C) The slope of this line is -3, it cannot be the required line. This option is not correct
D) The slope of this line is -3, it cannot be the required line. This option is not correct