Question

JK in the coordinate plane has endpoints with coordinates (-4, 11) and (8,

1)
Suppose J, P, and K are collinear on JK and JP:JK = }. What are the coordinates of P?
The coordinates of P are

Answer 1

(0, 7)

Explanation:

Given:

J(-4, 11)

K(8, -1)

JP:JK = 1/3

Required:

Coordinates of P

SOLUTION:

Use the formula,
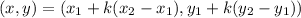`(x, y) = (x_1 + k(x_2 - x_1), y_1 + k(y_2 - y_1))` to find the coordinates of point P, that partition the segment JK into the ratio 1/3.

Let,

`J(-4, 11) = (x_1, y_1)`

`K(8, -1) = (x_2, y_2)`

`k = (1)/(3)`

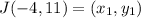
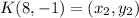
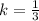
Thus, plug in the values as follows:

`P(x, y) = (-4 + (1)/(3)(8 -(-4)), 11 + (1)/(3)(-1 - 11)`

`P(x, y) = (-4 + (1)/(3)(12), 11 + (1)/(3)(-12)`

`P(x, y) = (-4 + (12)/(3), 11 + (-12)/(3))`

`P(x, y) = (-4 + 4, 11 + (-4)`

`P(x, y) = (0, 7)`

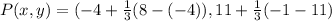
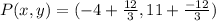
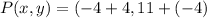
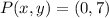
The coordinates of point P, are (0, 7)