Question

The sum of two consecutive odd integers is 2488 what is the smallest of these integers

Answer 1

Given:

The sum of two consecutive odd integers is 2488.

To find:

The smallest of these integers

Solution:

Let the two consecutive odd integers are x and x+2.

Given that, sum of these two consecutive odd integers is 2488. So,

`x+(x+2)=2488`

`2x+2=2488`

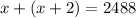
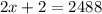
Subtract 2 from both sides.

`2x=2488-2`

`2x=2486`

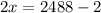
Divide both sides by 2.

`x=(2486)/(2)`

`x=1243`

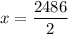
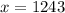
So, the first odd integer is 1243 and second odd integer is 1243+2=1245.

Therefore, the smallest of these integers is 1243.