Question

The Institute of Education Sciences measures the high school dropout rate as the percentage of 16- through 24-year-olds who are not enrolled in school and have not earned a high school credential. Last year, the high school dropout rate was 8.1%. A polling company recently took a survey of 1,000 people between the ages of 16 and 24 and found that 6.5% of them are high school dropouts. The polling company would like to determine whether the dropout rate has decreased. At a 5% significance level, the decision is to ________.

Answer 1

Explanation:

Given that:

The population proportion = 8.1% = 0.081

Sample size = 1000

The sample proportion
`\hat p` = 6.5% = 0.065

The null and the alternative hypothesis for these studies can be computed as:

`\mathbf{H_o : p = 0.081} \\ \\ \mathbf{H_1 : p \\eq 0.081}`

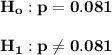
Since
`H_1` is not equal to the population proportion; then this is a two-tailed test.

The level of significance is given as 5% = 0.05

The standard error
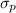`\sigma_p` of the sample proportion
`\hat p` can be computed as:

`\sigma_p = \sqrt{(p(1-p))/(n) }`

`\sigma_p = \sqrt{(0.081(1-0.081))/(1000) }`

`\sigma_p = \sqrt{(0.081(0.919))/(1000) }`

`\sigma_p = 0.0086`

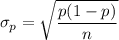
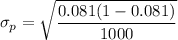
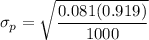
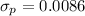
The z score test statistic is calculated as:

`z =(\hat p - p)/(\sigma_p)`

`z =(0.065- 0.081)/(0.0086)`

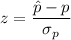
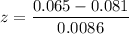
z = −1.860

For a two-tailed test, the p-value =
`2 * P(Z < -|z|)`

`p-value = 2 * P(Z < - 1.86)`

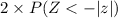
p-value = 2 × 0.0314

p-value = 0.0628

Rejection Criteria: To reject
`H_o` ; if the p-value is less than the level of significance ∝

The decision rule: We failed to reject the null hypothesis since the p-value is greater than the level of significance ∝.

Thus, there is insufficient evidence to conclude that p is not equal to 0.081