Question

Miller Corporation has a premium bond making semiannual payments. The bond has a coupon rate of 8 percent, a YTM of 6 percent, and 12 years to maturity. The Modigliani Company has a discount bond making semiannual payments. This bond has a coupon rate of 6 percent, a YTM of 8 percent, and also has 12 years to maturity. Both bonds have a par value of $1,000. What is the price of each bond today? (Do not round intermediate calculations. Round your answers to 2 decimal places, e.g., 32.16.) Price of Miller bond $ 1169.36 Price of Modigliani bond $ 847.53 If interest rates remain unchanged, what do you expect the price of these bonds to be 1 year from now? In 3 years? In 7 years? In 11 years? In 12 years?

Answer 1

Miller-bond:

today: $ 1,167.68

after 1-year: $ 1,157.74

after 3 year: $ 1,136.03

after 7-year: $ 1,084.25

after 11-year: $ 1,018.87

at maturity: $ 1,000.00

Modigliani-bond:

today: $ 847.53

after 1-year: $ 855.49

after 3 year: $ 873.41

after 7-year: $ 918.89

after 11-year: $ 981.14

at maturity: $ 1,000.00

Step-by-step explanation:

We need to solve for the present value of the coupon payment and maturity of each bonds:

Miller:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 80.000

time 12

rate 0.06

`80 * (1-(1+0.06)^(-12) )/(0.06) = PV\\`

PV $670.7075

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 12.00

rate 0.06

`(1000)/((1 + 0.06)^(12) ) = PV`

PV 496.97

PV c $670.7075

PV m $496.9694

Total $1,167.6769

In few years ahead we can capitalize the bod and subtract the coupon payment

after a year:

1.167.669 x (1.06) - 80 = $1,157.7375

after three-year:

1,157.74 x 1.06^2 - 80*1.06 - 80 = 1136.033855

If we are far away then, it is better to re do the main formula

after 7-years:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 80.000

time 5

rate 0.06

`80 * (1-(1+0.06)^(-5) )/(0.06) = PV\\`

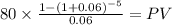
PV $336.9891

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 5.00

rate 0.06

`(1000)/((1 + 0.06)^(5) ) = PV`

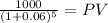
PV $747.26

PV c $336.9891

PV m $747.2582

Total $1,084.2473

1 year before maturity:

last coupon payment + maturity

1,080 /1.06 = 1.018,8679 = 1,018.87

For the Modigliani bond, we repeat the same procedure.

PV

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 30.000

time 24

rate 0.04

`30 * (1-(1+0.04)^(-24) )/(0.04) = PV\\`

PV $457.4089

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 24.00

rate 0.04

`(1000)/((1 + 0.04)^(24) ) = PV`

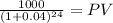
PV 390.12

PV c $457.4089

PV m $390.1215

Total $847.5304

And we repeat the procedure for other years