Answer:
Step-by-step explanation:
3% per year
monthly interest =
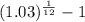
= 1.00246 -1 = .246 %
Present value of cash flow = 780 + 2000.37 + 3160.93 + 4264.62+ 5313.48
+ 6309.52 + 7254.67 + 8150.8 + 8999.71 + 9803.16 + 10562.85 + 11280.40
= 77880.51
capitalised cost for this cash outflow for indefinite period
= 77880.51 / .03 = 2596017
no of tickets = 1150000
price per ticket for break even
= 2596017 / 1150000
= 2.257
price per ticket for break even = 2.257