Answer:
Δt = 3.04 10³ s
Step-by-step explanation:
a) This is a thermal conduction exercise that is described by the expression
P = k A | dT/dx | (1)
where P power, k thermal conductivity, A the area, T the temperature and x the thickness
The power supplied to the wood is
P = Q / Δt
where the heat is given by
Q = m
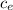 ΔT'
ΔT'
we substitute
P = m c_{e} ΔT'/ Δt
We assume that the changes in temperature and time can be approximated by their differences,
we substitute in 1
m c_{e} ΔT'/Δt = k A dT / dx
as the temperature changes are small, we can assume a linear variation, consequently the derivatives can be approximated to the variations
m ce ΔT'/Δt = k A ΔT/Δx (2)
let's write the temperature variations explicitly
ΔT’= (T_f -T₀)
ΔT’= 56 -0
ΔT =

ΔT = 70 -0
the thermal diffusivity is
α = k /ρ c_{e}
k = α c_{e}
the definition of density
ρ = m / V
ρ = m / A L
k = α c_{e} m / A L
we substitute in 2
m c_{e} Δx = (α c_{e} m / A L) A ΔT /ΔT' dt
Δx = α /L ΔT / ΔT’ Δt
Δt = L Dx /α ΔT'/ΔT
let's calculate
Δt = 2.54 1.27 10⁻⁴ / 8.5 10⁻⁸ (56- 0) / (70-0)
Δt = 3.04 10³ s