Question

answer the questions below, using lt (for is less than), gt (for is greater than), eq (for equal to), or mi (for more information) in the blanks provided. __________ 1. the wavelength of the photon required to promote an electron in the hydrogen atom from the n = 1 to the n = 3 level is __________ the wavelength of the photon required to promote an electron in the hydrogen atom from the n =1 to the n = 2 level. __________ 2. the energy of a photon with a wavelength of 463 nm is __________ the energy of a photon whose wavelength is 722 nm. __________ 3. in order to promote an electron to go to a higher energy level, light with a wavelength that is __________ 400 nm is required.

Answer 1

1. Given that the wavelength of the photon required to promote an electron in the hydrogen atom from the n = 1 to the n = 3 level is lt the wavelength of the photon required to promote an electron in the hydrogen atom from the n = 1 to the n = 2 level.

2. Given that the energy of a photon with a wavelength of 463 nm is gt the energy of a photon whose wavelength is 722 nm.

3. Therefore, in order to promote an electron to go to a higher energy level, light with a wavelength that is lt 400 nm is required

Step-by-step explanation:

The equation for electron transition in a hydrogen atom is given by the Rydberg equation as follows;

`(1)/(\lambda) = R * \left ((1)/(n^2_f) - (1)/(n^2_i) \right )`

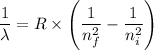
The energy required for electron transition is given by the formula;

`E = (h \cdot c)/(\lambda)`

`E = R_E * \left ((1)/(n^2_f) - (1)/(n^2_i) \right )`

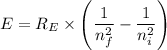
Where;

h = The Planck's constant

λ = The wavelength of light

c = The speed of light

n = Specific energy level

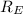`R_E` = -2.178 × 10⁻¹⁸ J

Therefore, the energy required to move an electron from one energy level to a higher energy level is inversely proportional to the wavelength of light, λ.

Increase in λ, results in lower energy available to transition to a higher energy level while a decrease in λ results in more energy available to transition to a higher energy level.