Question

PQ has endpoints P(-4, -2) and Q(-6, 8). What is the length of segment PQ in simplest radical form?

Answer 1

The answer is

`2 √(26) \: \: \: \: units`

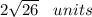
Explanation:

The distance between two points of a line segment can be found by using the formula

`d = \sqrt{ ({x_1 - x_2})^(2) + ({y_1 - y_2})^(2) } \\`

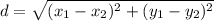
where

(x1 , y1) and (x2 , y2) are the points

From the question the points are

P(-4, -2) and Q(-6, 8)

The length of the line segment is

`|PQ| = \sqrt{ ({ - 4 + 6})^(2) + ({ - 2 - 8})^(2) } \\ = \sqrt{ {2}^(2) + ({ - 10})^(2) } \\ = √(4 + 100) \\ = √(104) \: \: \: \: \: \: \: \\ = 2 √(26) \: \: \: \: \: \: \:`

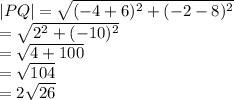
We have the final answer as

`2 √(26) \: \: \: \: units`

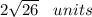
Hope this helps you