Answer:
Follows are the solution to this question:
Explanation:
In point a:
The weight difference between 5.29 lb and the weighted mean:
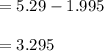
In point b:
The number of standard deviation:
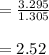
In point c:
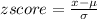
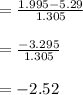
In point d:
No, since (-2, 2) included with the Zero is the z score and for weight is 5.29.