Answer:
The answer is below
Explanation:
Let t1 be the arrival times between a packet and its immediate predecessor and t2 be the arrival times between a packet and successor. Let L1 be the lengths of the predecessor packet and L2 the length of the packet itself. Therefore:
P(no collision between packet and predecessor or successor) =
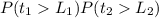
If P1 is the probability that there is no collision with preceding packets, hence:
P(no collision with other packets) =
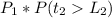
λ = 10 packets/s, fixed packet length = 20 ms = 0.02 s. Hence:
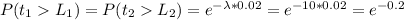
P(no collision between packet and predecessor or successor) =
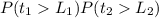 =
=

P(packet collides with either its predecessor or its successor) = 1 - P(no collision between packet and predecessor or successor) =
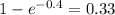
If the transmission times change, the answer would also change.