Question

2. The visible region of the hydrogen spectrum results from relaxation of electrons from excited states to energy level 2 (n1). Use the Rydberg equation and your measured wavelengths to determine the energy transitions associated with each of your observed wavelengths for hydrogen. In other words, calculate the excited state energy level (n2) for each of your observed wavelengths for hydrogen. n has integer values; so, calculate it first with appropriate significant digits, then round it to an integer. Use the key to show your work for at least one calculation. Must show energy levels for each hydrogen wavelength.

Answer 1

E = 1.89 eV , E = 2.56 eV , E = 2.86 eV

Step-by-step explanation:

The emission of light in the visible range, explained by the Balmer series with expression

1 /λ=
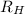`R_(H)` (1/2² - 1 / n²)

n = 3, 4, 5 ...

the constant R_{H} called Rydberg's constant and is equal to 1,097 10⁷ m⁻¹

These transitions are clearly explained by Bohr's atomic model, where the empirical series of Balmer and Rydberg are deduced from a theoretical model of the hydrogen atom in natural form.

Let's calculate the wavelengths for each transition

State

initial final λ (10⁻⁷ m)

3 2 6.5634

4 2 4.8617

5 2 4.3408

Let's calculate the energy of each of these wavelengths using Planck's equation

E = h f = h c /λ

λ = 6.5634 10⁻⁷ m

E = 6.63 10⁻³⁴ 3 10⁸ / 6.5634 10⁻⁷

E = 3.03 10⁻¹⁹ J

we reduce to eV

E = 3.03 10⁻¹⁹ J (1 eV / 1.6 10⁻¹⁹ J)

E = 1.89 eV

λ = 4.8617 10⁻⁷m

E = 6.63 10⁻³⁴ 3 10⁸ / 4.8617 10⁻⁷

E = 4.09 10⁻¹⁹ J

E = 2.56 eV

λ= 4.3408 10⁻⁷ m

E = 6.63 10⁻³⁴ 3 10⁸ / 4.3408 10⁻⁷

E = 4.582 10⁻¹⁹J

E = 2.86 eV