Answer:
Option (c)
Explanation:
Slope of a line that passing through two points M(-1, 4) and N(2, -5),
 =
=
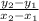
=
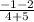
= -(
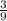 )
)
= -

To find the line perpendicular line to MN we will use the property,
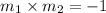
Where
 and
and
 are the slopes of two perpendicular lines.
are the slopes of two perpendicular lines.
Slope of line perpendicular to MN
 will be,
will be,
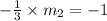
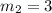
Slope of line joining two points J(-3, -4) and K(3, -2),
Slope =
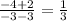
Slope of line joining two points A(-3, 2) and B(3, 0)
Slope =
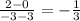
Slope of the line joining points E(0, -3) and F(2, 3),
Slope =
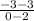 = 3
= 3
Therefore, line EF is perpendicular to the line MN.
Option (c) is the answer.