Question

Which line is perpendicular to a line that has a slope of -1/3?

a. line MN
b. line AB
c. line EF
d. line JK

Answer 1

Option (c)

Explanation:

Slope of a line that passing through two points M(-1, 4) and N(2, -5),

`m_1` =
`(y_2-y_1)/(x_2-x_1)`

=
`(-1-2)/(4+5)`

= -(
`(3)/(9)`)

= -
`(1)/(3)`

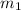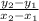
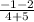
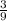To find the line perpendicular line to MN we will use the property,

`m_1* m_2=-1`

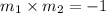
Where
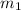`m_1` and
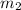`m_2` are the slopes of two perpendicular lines.

Slope of line perpendicular to MN
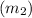`(m_2)` will be,

`-(1)/(3)* m_2=-1`

`m_2=3`

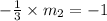
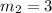
Slope of line joining two points J(-3, -4) and K(3, -2),

Slope =
`(-4+2)/(-3-3)=(1)/(3)`

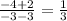
Slope of line joining two points A(-3, 2) and B(3, 0)

Slope =
`(2-0)/(-3-3)=-(1)/(3)`

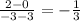
Slope of the line joining points E(0, -3) and F(2, 3),

Slope =
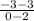`(-3-3)/(0-2)` = 3

Therefore, line EF is perpendicular to the line MN.

Option (c) is the answer.