Answer:
The listener is approximately 71.414 feet far from the whisperer.
Explanation:
We must remember that two fundamental variables for every ellipse are the major semiaxis (
 ) and the minor semiaxis (
) and the minor semiaxis (
 ). The major semiaxis equals a half of the length of the whispering gallery, whereas the minor semiaxis equals a half of the width of the whispering gallery. These are:
). The major semiaxis equals a half of the length of the whispering gallery, whereas the minor semiaxis equals a half of the width of the whispering gallery. These are:
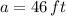 and
and
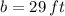
The distance between both whisperers (
 ), measured in feet, is two times the distance between center and any of the foci (
), measured in feet, is two times the distance between center and any of the foci (
 ), measured in feet, whose valued is obtained by using this Pythagorean identity:
), measured in feet, whose valued is obtained by using this Pythagorean identity:
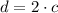
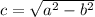
If
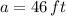 and
and
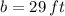 , then:
, then:
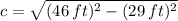
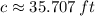
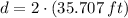
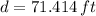
The listener is approximately 71.414 feet far from the whisperer.