Question

A 70​-m-long chain hangs vertically from a cylinder attached to a winch. Assume there is no friction in the system and that the chain has a density of 5 ​kg/m. Use 9.8 m/s2 for the acceleration due to gravity. a. How much work is required to wind the entire chain onto the cylinder using the​ winch? b. How much work is required to wind the chain onto the cylinder if a 35​-kg block is attached to the end of the​ chain?

Answer 1

a) The work required to wind the entire chain onto the cylinder using the winch is 120135.75 joules, b) The work required to wind the chain plus the block is 144162.9 joules.

Step-by-step explanation:

a) Let be an infinitesimal part of the long chain, whose gravitational potential energy is:

`dU_(g) = g\cdot z \,\delta m`

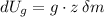
Where:

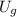`U_(g)` - Gravitational potential energy, measured in joules.

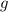`g` - Gravitational acceleration, measured in meters per square second.

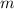`m` - Mass of the long chain, measured in kilograms.

`z` - Height of the portion of the long chain with respect to ground, measured in meters.

Since chain has an uniform linear density, this differential expression can be rewritten as:

`dU_(g) = \lambda\cdot g \cdot z \, dz`

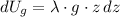
Where
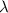`\lambda` is the linear density, measured in kilograms per meter.

We obtain the gravitational potential energy to wind the chain onto the cylinder by integration:

`\Delta U_(g, chain) = \lambda\cdot g \int\limits^{z_(f)}_{z_(o)} {z} \, dz`

`\Delta U_(g, chain) = (\lambda\cdot g)/(2) \cdot (z_(f)^(2)-z_(o)^(2))`

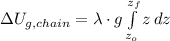
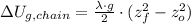
Where:

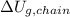`\Delta U_(g, chain)` - Gravitational potential energy of the entire chain, measured in joules.

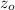`z_(o)` - Initial height with respect to ground, measured in meters.

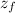`z_(f)` - Final height with respect to ground, measured in meters.

From the Work-Energy Theorem we get that work needed to wind the entire chain equals the gravitational potential energy of the entire chain:

`W = \Delta U_(g, chain)`

`W = (\lambda\cdot g)/(2) \cdot (z_(f)^(2)-z_(o)^(2))`

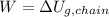
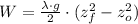
If we know that
`\lambda = 5\,(kg)/(m)`,
`g = 9.807\,(m)/(s^(2))`,
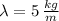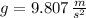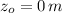`z_(o) = 0\,m` and
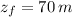`z_(f) = 70\,m`, the work needed is:

`W = (\left(5\,(kg)/(m) \right)\cdot \left(9.807\,(m)/(s^(2)) \right))/(2) \cdot [(70\,m)^(2)-(0\,m)^(2)]`

`W = 120135.75\,J`

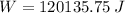
The work required to wind the entire chain onto the cylinder using the winch is 120135.75 joules.

b) The gravitational potential energy of the block, measured in joules, is:

`\Delta U_(g,block) = m_(block)\cdot g \cdot (z_(f)-z_(o))`

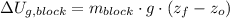
Where:

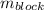`m_(block)` - Mass of the block, measured in kilograms.

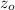`z_(o)` - Initial height with respect to ground, measured in meters.

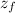`z_(f)` - Final height with respect to ground, measured in meters.

According to the Work-Energy Theorem, the work needed to wind the chain plus the block equals the sum of both gravitational potential energies:

`W = \Delta U_(g, chain)+U_(g,block)`

`W = (\lambda \cdot g)/(2)\cdot (z_(f)^(2)-z_(o)^(2))+m_(block)\cdot g \cdot (z_(f)-z_(o))`

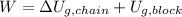
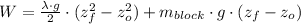
If we know that
`\lambda = 5\,(kg)/(m)`,
`g = 9.807\,(m)/(s^(2))`,
`z_(o) = 0\,m`,
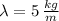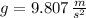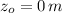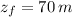`z_(f) = 70\,m` and
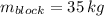`m_(block) = 35\,kg`, the work required to wind the chain onto the cylinder if a block is attached to the end of the chain is:

`W = (\left(5\,(kg)/(m) \right)\cdot \left(9.807\,(m)/(s^(2)) \right))/(2)\cdot [(70\,m)^(2)-(0\,m)^(2)]+(35\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (70\,m-0\,m)`

`W = 144162.9\,J`

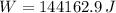
The work required to wind the chain plus the block is 144162.9 joules.