Question

(Ch10.7) True or False? Based on a random sample of 13 tire changes (n1), the mean time to change a tire on a Boeing 777 has a mean of 59.5 minutes with a standard deviation of 7.4 minutes. For 10 tire changes (n2) on a Boeing 787, the mean time was 64.3 minutes with a standard deviation of 13.2 minutes. In testing equal variances in a "two-tailed" F-test at α=0.1, we should reject the null hypothesis of equal population variances.

Answer 1

Yes its true

Calculated value F = 3.264 > 2.32 at 0.1 level of significance

Null hypothesis is rejected

alternative hypothesis is accepted

The population variances are not equal

Explanation:

Step(i):-

Given first sample size 'n₁ = 13

Mean of the first sample = 59.5 min

Standard deviation of the first sample (S₁) = 7.4min

Mean of the second sample = 64.3 min

Standard deviation of the second sample( S₂ ) = 13.2min

Null hypothesis :H₀: σ₁² = σ₂²

Alternative Hypothesis : H₁ : σ₁² ≠ σ₂²

Degrees of freedom

ν₁ = n₁ -1 = 13 -1 = 12

ν₂ = n₂ -1 = 10 -1 = 9

Step(ii):-

Null Hypothesis H₀ : σ₁² = σ₂²

Alternative Hypothesis : H₁ : σ₁² ≠ σ₂²

Test statistic

`F = (S_(2) ^(2) )/(S^(2) _(1) )`

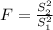
Given sample standard deviations are given

we have to determine the Population variances S₁² and S₂²

n₁ s₁² = (n₁-1) S₁²

13 ( 7.4)² = ( 13-1) S₁²

S₁² = 59.32

n₂ s₂² = (n₂-1) S₂²

10 ( 13.2)² = ( 10-1) S₂²

S₂² = 193.6

Step(iii):-

Test statistic

`F = (S_(2) ^(2) )/(S^(2) _(1) ) = (193.6)/(59.3) = 3.264`

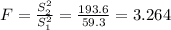
F = 3.264

F( 12 , 9 ) = 2.32

Calculated value F = 3.264 > 2.32 at 0.1 level of significance

Null hypothesis is rejected

alternative hypothesis is accepted

The population variances are not equal