Question

A circular loop has a radius of .3 meters a magnetic field has an initial strength of 2 tesla directed out of the page. over the course of 5 seconds the magnetic field is changed to 3 tesla directed out of the page calculate the induced voltage in the loop

Answer 1

Hi there!

We can use Faraday's Law to solve:

`\epsilon = N(d\Phi _B)/(dt)`

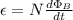
ε = Induced emf (? V)

N = Number of loops (1 loop)

ΦB = Magnetic flux (Wb)

We know that:

`\Phi_B = \oint B \cdot dA = B\cdot A`

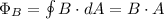
Since the area of the loop remains the same, we can take this out of the time derivative.

We get:

`(d\Phi_B)/(dt) = A * (dB)/(dt)`

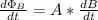
Also, since N = 1, we can now rewrite the equation for the induced emf as:

`\epsilon = A * (dB)/(dt)`

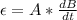
dB/dt is equivalent to the change in the magnetic field with respect to time:

`\Delta B = (B_f - B_i)/(\Delta t)\\\\\Delta B = (3 - 2)/(5) = 0.2 (T)/(s)`

Now, substitute this value into the equation for induced emf:

`\epsilon = \pi (0.3^2) * (0.2) = \boxed{0.0565 V}`

**Also, since the magnetic field INCREASED out of the page, this change in magnetic flux will create an induced CLOCKWISE current that produces a magnetic field into the page in order to oppose the increase in magnetic flux OUT of the page.