Hi there!
We can use Faraday's Law to solve:
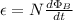
ε = Induced emf (? V)
N = Number of loops (1 loop)
ΦB = Magnetic flux (Wb)
We know that:
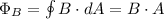
Since the area of the loop remains the same, we can take this out of the time derivative.
We get:
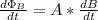
Also, since N = 1, we can now rewrite the equation for the induced emf as:
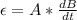
dB/dt is equivalent to the change in the magnetic field with respect to time:
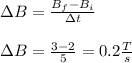
Now, substitute this value into the equation for induced emf:
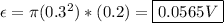
**Also, since the magnetic field INCREASED out of the page, this change in magnetic flux will create an induced CLOCKWISE current that produces a magnetic field into the page in order to oppose the increase in magnetic flux OUT of the page.