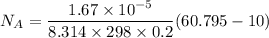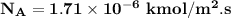Question

The gas CO2 is diffusing at steady state through a tube 0.20 meters long. The tube has a diameter of 0.01 meters and also contains N2 at 298 K. The total pressure inside the tube is constant at 101.32 kPa. The partial pressure of CO2 is 456 mm Hg at one end and 76 mm Hg at the other end. The diffusion coefficient of CO2 in N2 is 1.67 x 10-5 m2 /sec at 298 K. Calculate the molar flux of CO2 in SI units, assuming equimolar counter-diffusion between the CO2 and N2 gases.

Answer 1

`\mathbf{N_A = 1.71 * 10^(-6) \ kmol/m^2.s}`

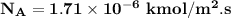
Step-by-step explanation:

From the given information:

The total length = 0.20 m

Diameter = 0.01 m

Temperature = 298 K

Pressure = 101.32 kPa

The partial pressure of CO2 i.e
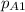`p_(A1)` is 456 mm Hg at one end

To kPa, we have:

=
`456 * (101.325)/(760)`

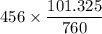
= 60.795 kPa

The partial pressure of CO2 i.e.
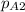`p_(A2)` at the other end is 76 mm Hg

To kPa; we have

=
`75 * (101.325)/(760)`

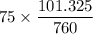
= 9.999 kPa

`\simeq` 10 kPa

The diffusion coefficient of CO
`_2` in N
`_2` is 1.67 × 10⁻⁵

Universal gas constant = 8.314 J/mol/k

For equimolar counter-diffusion between the CO2 and N2 gases, the molar flux of CO
`_2` can be estimated by using the formula:

`N_A = (D_(AB))/(RT)(p_(A1) - p_(A2))`

replacing our values from the above parameters then:

`N_A = (1.67 * 10^(-5))/(8.314 * 298 * 0.2)(60.795 - 10)`

`\mathbf{N_A = 1.71 * 10^(-6) \ kmol/m^2.s}`