Question

A trough is 8m long and has ends which are isosceles triangles with height 3m and width (across the top) of 3m. The trough has a spout at the top of the tank with height 2m. The tank is full of water. (a) How much work is required to pump all of the water out of the tank? (NOTE that the density of water is rho = 1000 kg/m3 and the acceleration due to gravity is 9.8 m/s2 . (b) Suppose the pump breaks down after 4 × 105 J of work has been done. What is the depth of the remaining water in the tank

Answer 1

(a) the work required to pump all of the water out is 1.0584 x 10⁶ J

(b) the depth of the remaining water in the tank is 1.87 m

Step-by-step explanation:

Given;

length of trough, L = 8m

height of the isosceles triangle, h = 3m

width of the isosceles triangle, w = 3m

length of spout, b = 2m

The center mass of isosceles triangle is given by;

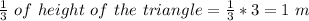`(1)/(3) \ of \ height \ of \ the \ triangle = (1)/(3) *3 = 1 \ m` (this is the height below the top of the trough)

The total height water will be pumped, H = 1m + b

H = 1m + 2m = 3m

Determine the volume of the trough;

Volume of the trough = area of the triangle x length of the trough

Volume of trough =
`(1)/(2)*3*3*(8) = 36 \ m^3`

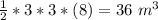
(a) The work done in pumping all of the water out;

The work done in pumping all of the water out = potential energy of water at that height, H;

W = mgH

where;

m is mass of water

m = ρV

m = (1000 kg/m³) x (36 m³)

m = 36,000 kg

The work done = mgH

= 36,000 x 9.8 x 3

= 1.0584 x 10⁶ J

(b) after 4 × 10⁵ J of work has been done, the energy required to pump out the remaining water is given by;

ΔE = 1.0584 x 10⁶ J - 4 × 10⁵ J = 658,400 J

The depth of the remaining water is calculated as

658,400 J = mgh

where;

h is the height of the remaining water

658,400 = (36,000 x 9.8)h

658,400 = 352,800h

h = 658,400 / 352,800

h = 1.87 m