Answer:
The equation that model the projectile's height is

Explanation:
We know that projectile is fired vertically upward from a height of 200 feet above the ground with an initial velocity of 900 feet per second and projectiles experiment a parabolic motion, which combines horizontal uniform motion and vertical uniform accelerated motion due to gravity, whose equation of motion is:
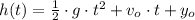
Where:
 - Current height above the ground at instant t, measured in feet.
- Current height above the ground at instant t, measured in feet.
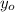 - Initial height, measured in feet.
- Initial height, measured in feet.
 - Initial velocity, measured in feet per second.
- Initial velocity, measured in feet per second.
 - Gravitational acceleration, measured in feet per square second.
- Gravitational acceleration, measured in feet per square second.
 - Time, measured in seconds.
- Time, measured in seconds.
If we know that
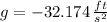 ,
,
 and
and
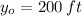 , the equation that model the projectile's height is
, the equation that model the projectile's height is
