Question

g farmer brown wants to upgrade the fencing around his rectangular pasture.he would like to put a stone fence along one (1) side and a wooden fence along the other three (3) sides. the cost of the stone fence is $100 per linear foot, and the cost of the wooden fence is $20 per linear foot. a. if the pasture must have an area of 7,500 square feet, what are the dimensions of the field which will minimize the cost of the fencing

Answer 1

The answer is below

Explanation:

Let x represent the length of the fence along the stone side and y represent the length of the fence along the wood side. The cost of building the fence C(x) is given by:

C(x) = 100x + 20(2y + x)

C(x) = 100x + 40y + 20x

C(x) = 120x + 40y

Since the area = 7500 ft²,

⇒ xy = 7500

y = 7500/x

`C(x) = 120x + 40((7500)/(x) )\\\\C(x) = 120x+(300000)/(x)\\ \\Differentiating\ with\ respect\ to\ x:\\\\C'(x) =120-(300000)/(x^2) \\\\At\ minimum\ cost,C(x)=0\\\\hence:\\\\0=120-(300000)/(x^2)\\\\(300000)/(x^2)=120\\\\120x^2=300000\\\\x^2=(300000)/(120)\\ \\x^2=2500\\\\x=√(2500) \\\\x=50\ ft`

`C`

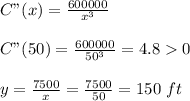
Hence to minimize cost, 50 ft of fence is used along the stone side and 150 ft of fence along the wood side