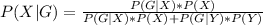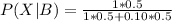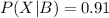Question

The perpetrator is either one or the other of the two persons X and Y. Both persons are on the run from the authorities, and after an initial investigation, both fugitives appear equally likely to be the perpetrator. Further investigation reveals that the actual perpetrator has blood type A. 10% of the population has blood type A; you may assume that the innocent one of persons X and Y has a 10% chance of having blood type A. In the investigation, you find two samples of blood; the first sample belongs to person X, and the second sample belongs to person Y. In the process of testing the blood, the sample belonging to person Y was accidentally destroyed (you may assume that the destruction was random). The sample belonging to person X was determined to be blood type A. In light of this new information, find the probability that person X is the perpetrator

Answer 1

The probability is
`P(X | B) = 0.91`

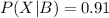
Explanation:

Generally the probability of the perpetrator being X is equal to the probability of the perpetrator being Y (given that both fugitives appear equally likely to be the perpetrator )

This can be mathematically represented as

`P(X) = P(Y) = (1)/(2)`

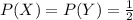
Let G represent the event that the blood type of the sample is type A

Generally if X has a blood type A then it is almost certain that the perpetrator is X compared to Y

This can be mathematically represented as

`P(G | X) = 1`

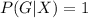
( Here this means the probability of the sample being of type A given that the X has a blood type A )

Given that the sample belonging to Y accidentally destroyed

Then the probability that Y is innocent given that the blood type of Y is of type A

This can be mathematically represented as

`P(G | Y) = 10\%`

`P(G | Y) = 0.10`

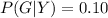
Generally according to Bayes rule the probability that person X is the perpetrator mathematically as

`P(X | G) = (P(G|X) * P(X))/( P(G|X) * P(X) + P(G | Y ) * P(Y))`

`P(X | B) = (1 * 0.5 )/( 1 * 0.5 + 0.10 * 0.5)`

`P(X | B) = 0.91`