Question

An rescue airplane flies horizontally over level terrain with a speed of 251 m/s and at an altitude of 2.73 km. The airplane releases one package. (a) How far does the package travel horizontally between its release and its impact on the ground? Ignore air resistance. m (b) If the pilot maintains the airplane's original course, altitude, and speed, where will the plane be when the package hits the ground? Ignore air resistance. behind the bomb directly above the bomb ahead of the bomb (c) The package hits the target seen in the airplane's telescopic "bombsight" at the moment of the package's release. At what angle from the vertical was the bombsight set? ° from the vertical

Answer 1

a) x = 5923.6 m , b) directly above the bomb ahead of the bomb,

c) θ = 65.3º

Step-by-step explanation:

This is a projectile launching exercise

a) As the package is released from the plane at its same speed, vox 0 251 m / s, they indicate that the plane flies horizontally, therefore the initial vertical speed is zero, let's calculate the time of arrival to the ground

y = y₀ +
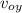`v_(oy)` t - ½ g t²

to the ground y = 0

0 = y₀ + 0 - ½ g t²

t = √ (2y₀ / g)

t = √ (2 2730 / 9.8)

t = 23.60 s

the horizontal distance traveled is

x = v₀ₓ t

x = 251 23.6

x = 5923.6 m

b) since there is no acceleration on the x-axis and it is indicated that the air resistance is zero in part it must be just below the plane

directly above the bomb ahead of the bomb

c) for this part we can use trigonometry

since the angle with respect to the vertical is requested, the opposite leg is the horizontal distance

tan θ = x / y

θ = tan⁻¹ (x / y)

θ = tan⁻¹ (5923.6 / 2730)

θ = 65.3º