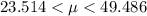Complete Question
A 95% confidence interval of 19.3 months to 47.5 months has been found for the mean duration of? imprisonment, ??,of political prisoners of a certain country with chronic PTSD.
a. Determine the margin of error, E.
b. Explain the meaning of E in this context in terms of the accuracy of the estimate.
c. Find the sample size required to have a margin of error of 13 months and a 99% confidence level.? (Use 38 months. for standard deviation )
d. Find a 99% confidence interval for the mean duration of? imprisonment, ??, if a sample of the size determined in part? (c) has a mean of 36.5 months.
Answer:
a

b
In this context E tell us that the true mean will lie within E = 14.1 of the sample mean
c
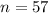
d
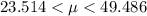
Explanation:
Considering question a
From the question we are told that
The upper limit is U = 47.5 months
The lower limit is L = 19.3 months
Generally the margin of error is mathematically represented as
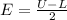
=>
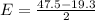
=>

Considering question b
In this context E tell us that the true mean will lie within E = 14.1 of the sample mean
Considering question c
Generally the sample size is mathematically represented as
![n = [ \frac{ Z_{(\alpha )/(2) * \sigma }}{ E} ]^2](https://img.qammunity.org/2021/formulas/mathematics/college/etjel29cnfh9mz6ehffzl9wkei910p51wf.png)
Here E is given as E = 13
Given that the confidence level is 99% then the level of significance is
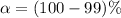
=>

From the normal distribution table the critical value of
 is
is
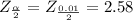
So
![n = [ (2.58 * 38)/(13)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/ju1i7ra5fhtzuzgb9vh6van8cqdcf8pu1c.png)
=>
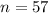
Considering question d
From the question
The sample mean is
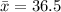
Generally the margin of error is mathematically represented as
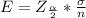
=>
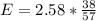
=>
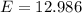
Generally the 99% confidence interval for mean distribution is mathematically represented as
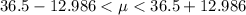
=>