Step-by-step explanation:
Given that,
Radius of a spherical shell, r = 0.71 m
Electric field that points radially toward the center of the sphere is 936 N/C
(a) Let q is the net charge within the sphere's surface. Using Gauss's law, we can find it :
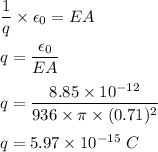
(b) Gauss's law is used to find the amount of charge enclosed within a surface. It doesn't say anything about the distribution of the charge inside the spherical shell.