Question

asked Aug 12, 2021 47.2k views

2 Answers

Flodin · Answer 1 · 2021-08-18T09:22:08+0000

Answer:

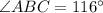
$\angle ABC=116\textdegree$

Explanation:

Remember that by the definition of angle bisector, the two resulting angles are equivalent to each other.

So, ∠CBD and ∠ABD are equivalent. In an equation:

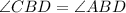
$\angle CBD=\angle ABD$

Substitute them for their equations:

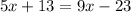
5x+13=9x-23

Solve for x. Add 23 to both sides:

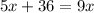
5x+36=9x

Subtract 5x from both sides:

36=4x

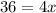
Divide both sides by 4:

x=9

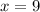
So, the value of x is 9.

Now, to find ∠ABC, note that it is the sum of ∠CBD and ∠ABD. So:

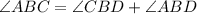
$\angle ABC=\angle CBD+\angle ABD$

Since we know the two angles are equivalent, we can substitute:

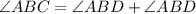
$\angle ABC=\angle ABD+\angle ABD$

We can combine like terms:

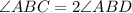
$\angle ABC=2\angle ABD$

Substitute ∠ABD for the equation. This gives us:

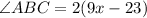
$\angle ABC=2(9x-23)$

Substitute 9 for x. So:

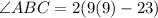
$\angle ABC=2(9(9)-23)$

Multiply:

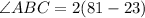
$\angle ABC=2(81-23)$

Subtract:

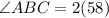
$\angle ABC=2(58)$

Multiply:

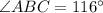
$\angle ABC=116\textdegree$

And we're done!

Please log in or register to add a comment.