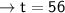Question

Radioactive iodine treatment is so successful at treating hyperthyroidism that it has virtually replaced thyroid surgery. To the nearest full day, determine how long it will take for 400 milicuries of -131, which

has a half-life of 8 days, to decay to 3.125 millicuries.
o 7 days
o 8 days
56 days
o 128 days

Answer 1

56 days

Step-by-step explanation:

`\sf Half \ Life : A = A_O \ x \ ((1)/(2) )^{(t)/(h) }`

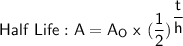
where A is final amount, Ao is initial amount, t is time taken, h is half life

Here given:

initial amount: 400 millicuries

final amount: 3.125 millicuries

half life: 8 days

time taken: ?

Hence solve for time taken:

`\sf \rightarrow A = A_O \ x \ ((1)/(2) )^{(t)/(h) }`

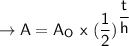
insert values given

`\sf \rightarrow 3.125 = 400 \ x \ ((1)/(2) )^{(t)/(8) }`

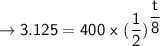
divide both sides by 400

`\sf \rightarrow ((1)/(2))^{(t)/(8)}=0.0078125`

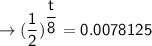
apply exponent rule

`\sf \rightarrow {(t)/(8)}=(ln(0.0078125))/(ln(1/2))`

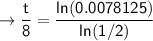
simplify

`\rightarrow \sf (t)/(8)=7`

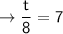
multiply both sides by 8

`\rightarrow \sf t = 56`