Given:
The inequality is
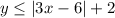 .
.
Alisha solved the given inequality and got
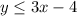 for
for
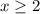 and
and
 for
for
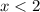 .
.
To find:
The Alisha's error, and the correct answer.
Solution:
We have,
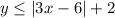
For
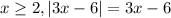 . So,
. So,
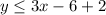
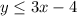
For
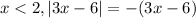 . So,
. So,
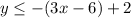
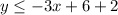
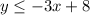
Alisha's second inequality is wrong because she did not distribute the negative with 6.
Therefore, the correct answer is
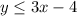 for
for
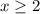 and
and
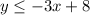 for
for
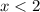 .
.