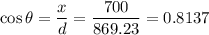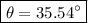Question

1. A rectangular field has one side fence 500 meters long, and another side fence

700 meters long
What is the length of a diagonal across the field?
b. What is the angle between the diagonal and the long side fence?
a

Answer 1

`d=860.23\ m`

`\theta=35.54^\circ`

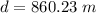
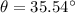
Explanation:

Rectangles

The sides of the rectangular fields are 500 meters and 700 meters. The diagonal of the rectangle can be calculated as the hypotenuse of the right triangle formed by the two sides, thus:

`d=√(x^2+y^2)`

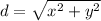
Where x and y are the lengths of the sides. For the rectangular field, we have:

`d=√(500^2+700^2)=√(250000+490000)=√(740000)=860.23\ m`

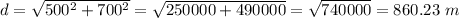
The angle between the diagonal and the longest side can be calculated using trigonometry. Please refer to the image attached.

`\displaystyle \cos\theta=(x)/(d)=(700)/(869.23)=0.8137`

`\boxed{\theta=35.54^\circ}`