Answer:
The points that are 10 units from P(-17,-2) are (-23,6) and (-11,6)
Explanation:
Distance Between Points in the Plane
Given two points A(x,y) and B(w,z), the distance between them is:
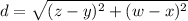
It can be also expressed as:
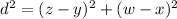
Substituting the values of both points, and knowing the distance is 10:
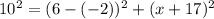
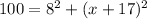
Swapping both sides:

Moving the constants to the right side:
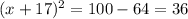
Taking the square root:
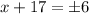
We get two possible answers:
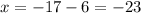
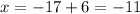
Thus the points that are 10 units from the point P(-17,-2) are (-23,6) and (-11,6)