Question

When jumping, a flea accelerates at an astounding 1000 m/s2, but over only the very short distance of 0.42 mm. If a flea jumps straight up, and if air resistance is neglected (a rather poor approximation in this situation), how high does the flea go? Express your answer in two significant figures.

Answer 1

h = 0.0428 [m] = 42.81 [mm]

Step-by-step explanation:

In order to solve this problem, we must divide it into two parts. In the first part we analyze the kinematics to find the initial speed with which the flea takes off from the ground. This initial speed can be found by the following expression:

`v_(f)^(2) = v_(i)^(2) -(2*a*y)\\`

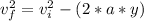
where:

a = acceleration = 1000 [m/s^2]

y = distance = 0.42[mm] = 0.00042 [m]

vf = final velocity = 0

vi = initial velocity [m/s]

It is important to define that when the flea reaches the maximum height its final speed is zero, because its movement has ended. It should also be said that the negative sign of the equation demarcates that the gravitational acceleration is contrary to the movement of the flea.

0 = vi^2 - (2*1000*0.00042)

vi = 0.9165 [m/s]

In the second part of this problem the conservation of energy will be taken, that is, the kinetic energy will be transformed into potential energy, thus reaching the next equality.

`m*g*h=(1)/(2) *m*v^(2) _(i)`

where:

m = mass of the flea

g = gravitational acceleration [m/s^2]

h = elevation [m]

vi = initial velocity [m/s]

h = (0.5*(0.9165)^2)/9.81

h = 0.0428 [m] = 42.81 [mm]