Answer:
Approximately
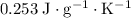 assuming no heat exchange between the mixture and the surroundings.
assuming no heat exchange between the mixture and the surroundings.
Step-by-step explanation:
Consider an object of specific heat capacity
 and mass
and mass
 . Increasing the temperature of this object by
. Increasing the temperature of this object by
 would require
would require
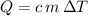 .
.
Look up the specific heat of water:
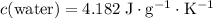 .
.
It is given that the mass of the water in this mixture is
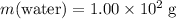 .
.
Temperature change of the water:
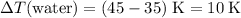 .
.
Thus, the water in this mixture would have absorbed :
 .
.
Thus, the energy that water absorbed was:
 .
.
Assuming that there was no heat exchange between the mixture and its surroundings. The energy that the water in this mixture absorbed,
 , would be the opposite of the energy that the metal in this mixture released.
, would be the opposite of the energy that the metal in this mixture released.
Thus:
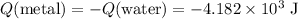 (negative because the metal in this mixture released energy rather than absorbing energy.)
(negative because the metal in this mixture released energy rather than absorbing energy.)
Mass of the metal in this mixture:
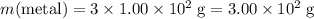 .
.
Temperature change of the metal in this mixture:
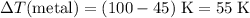 .
.
Rearrange the equation
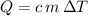 to obtain an expression for the specific heat capacity:
to obtain an expression for the specific heat capacity:
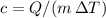 . The (average) specific heat capacity of the metal pieces in this mixture would be:
. The (average) specific heat capacity of the metal pieces in this mixture would be:
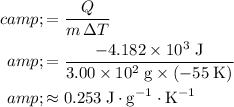 .
.