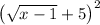Question

I’m Really lost if I could get a answer it would be greatly appreciated

Answer 1

Answers:

`f(g(x)) = √(x^2+5)+5\\\\g(f(x)) = x+30+10√(x-1)`

================================================

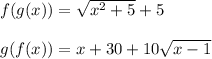
Work Shown:

Part 1

`f(x) = √(x-1)+5\\\\f(g(x)) = √(g(x)-1)+5\\\\f(g(x)) = √(x^2+6-1)+5\\\\f(g(x)) = √(x^2+5)+5\\\\`

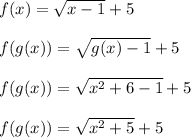
Notice how I replaced every x with g(x) in step 2. Then I plugged in g(x) = x^2+6 and simplified.

------------------

Part 2

`g(x) = x^2+6\\\\g(f(x)) = \left(f(x)\right)^2+6\\\\g(f(x)) = \left(√(x-1)+5\right)^2+6\\\\g(f(x)) = \left(√(x-1)\right)^2+2*5*√(x-1)+\left(5\right)^2+6\\\\g(f(x)) = x-1+10√(x-1)+25+6\\\\g(f(x)) = x+30+10√(x-1)\\\\`

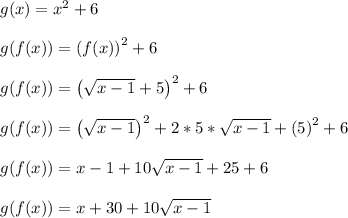
In step 4, I used the rule (a+b)^2 = a^2+2ab+b^2

In this case, a = sqrt(x-1) and b = 5.

You could also use the box method as a visual way to expand out
`\left(√(x-1)+5\right)^2`