Question

A-domain: positive integers; range: positive integers; No, it is not a function.

B-domain: x ≥ 0; range: y > –3; No, it is not a function.
C-domain: all real numbers; range: all real numbers; Yes, it is a function.
D-domain: x > –3; range: y > 0; Yes, it is a function.

PLEASE SHOW WORK

Answer 1

Answer: y>0

Explanation:

Let's look at the graph. If we do the vertical line test, we can figure out that YES, it is a function, so option b and c are already out of the picture.

Now, to find the domain, look at the graph and shade it back to the x-axis. The domain includes every number greater than 3, so the domain is x>3.

To find the range, take a look at the graph and shade it back to the y-axis. The range includes every real number greater than 0, so the range is y>0

This means that d is the answer.

I really hope this helps!

Best wishes :)

Answer 2

D

Explanation:

The domain of a function is the span of x-values it covers, while the range of a function is the span of y-values it covers.

DOMAIN:

We can see that the graph covers all x-values to the right of x=-3.

However, at exactly x=-3, the graph goes upwards infinitely. So, we say that there is a vertical asymptote at x=-3. Therefore, x=-3 is not included in our domain.

So, our domain is only all values greater than -3.

As an inequality, this is:

`x>-3`

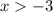
RANGE:

We can see that the graph covers all y-values until y=0.

At y=0, we have a horizontal asymptote.

Therefore, our y-values will never touch y=0.

So, our range are all values greater than 0.

In an inequality, this is:

`y>0`

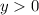
To determine if a function is a function, we can use the vertical line test.

If we draw a vertical line anywhere on the graph, it should not cross the graph more than once.

We can see that no matter where we draw our vertical line, it will only cross the graph once. This may be hard to see with the vertical asymptote, but the vertical asymptote will never be completely vertical despite its name.

So, this is indeed a function.

The answer choices that reflects these answers is D.

So, our answer is D.

And we're done!