Question

Hey guys...I really need help on this... Compare the original figure to the enlarged figure. Which ratios can be used to find the scale factor? Check all that apply.

Please don't copy google or others websites...
I'm giving out more points again...

Answer 1

A and C

Explanation:

Answer 2

A and C.

Explanation:

Remember that to find the scale factor, we can write a ratio between each of the corresponding sides.

In other words, the scale factor k will be:

`k=\frac{\text{Enlarged Side}}{\text{Corresponding Original Side}}`

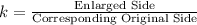
Most importantly, their sides must be corresponding.

So, let's go through each of the answer choices.

A)

We have:

`k=\frac{\text{Enlarged}}{\text{Original}}=(6.5)/(3.25)`

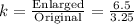
In our figures, we can see that 6.5 from our scaled figure indeed corresponds to 3.25 from our original figure. So, A is correct.

B)

We have:

`k=\frac{\text{Enlarged}}{\text{Original}}=(3.25)/(6.5)`

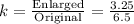
This is not correct because 3.25 is our original, not our enlarged. It should be flipped, like choice A. So, B is not correct.

C)

We have:

`k=\frac{\text{Enlarged}}{\text{Original}}=(3)/(1.5)`

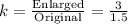
We can see that 3 from our enlarged figure indeed corresponds with 1.5 from our original figure. So, choice C is also correct.

D)

We have:

`k=\frac{\text{Enlarged}}{\text{Original}}=(1.5)/(3)`

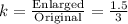
Similarly to B, this is not correct because our enlarged number should be in the numerator while our original number should be in the denominator. So, D is not correct.

E)

We have:

`k=\frac{\text{Enlarged}}{\text{Original}}=(1.5)/(3.25)`

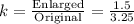
This is not correct because the sides do not represent the scaled figure. Both of the given side lengths are from the original figure, and so we cannot determine the scale factor from this.

So, our final answers are A and C.

And we're done!