Question

The total volume required to reach the endpoint of a titration required more than the 50 mL total volume of the buret. An initial volume of 49.17±0.04 mL was delivered, the buret was refilled, and an additional 1.56±0.04 mL was delivered before the endpoint was reached. The titration of a blank solution without the analyte required 0.60±0.04 mL . Calculate the endpoint volume corrected for the blank and its absolute uncertainty. Note: Significant figures are graded for this problem. To avoid rounding errors, do not round your answers until the very end of your calculations. volume: mL ± mL

Answer 1

The answer is "
`\bold{50.42 \pm 0.08}`".

Step-by-step explanation:

Overall delivered volume
`= [(49.06 \pm 0.05) + (1.77 \pm 0.05)]\ mL`

Its blank solution without any of the required analysis
`= (0.41 \pm 0.04)\ mL`

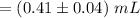
Compute the volume of the endpoint as follows:

Formula:

`\text{End point volume = Total Volume delivered - volume required}`

`= (49.06 \pm 0.05) + (1.77 \pm 0.05) - (0.41 \pm 0.04) \\\\= (49.06 + 1.77 - 0.41) \pm \ \ (absolute \ \ uncertainty)`

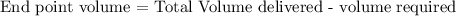
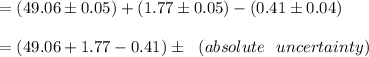
therefore,

absolute uncertainty
`=√((0.05)^2 + (0.05)^2 + (0.04)^2)`

`=√(0.0025 +0.0025 +0.0016) \\ \\=√(0.0066)\\\\=0.08124\\`

The Endpoint volume
`= (49.06+1.77-0.41)\pm (0.08124)`

`= 50.42 \pm 0.08`

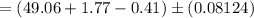
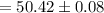
Therefore, the volume of the endpoint adjusted for the blank is:

`\bold { = 50.42 \pm 0.08}`