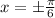Answer: Choice C.
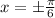
=========================================================
Step-by-step explanation:
Recall that
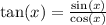
So we can say
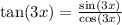
The vertical asymptotes occur when the denominator is zero.
If we were to plug in
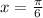 , then we'd have,
, then we'd have,
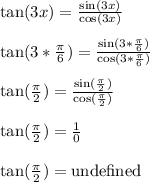
This shows that one vertical asymptote is at
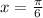
Through similar steps, you should find that another vertical asymptote is at
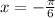
We can condense those two equations into