Question

A ping pong ball is drawn at random from an urn consisting of balls numbered 2 through 10. A player wins 1 dollar if the number on the ball is odd and loses 1 dollar if the number is even. What is the expected value of his winnings? Express your answer in fraction form.

Answer 1

Given:

A ping pong ball is drawn at random from an urn consisting of balls numbered 2 through 10.

A player wins 1 dollar if the number on the ball is odd and loses 1 dollar if the number is even.

To find:

The expected value of his winnings.

Solution:

Balls numbered 2 through 10. So, numbers are 2, 3, 4, 5, 6, 7, 8, 9, 10.

Odd numbers = 3, 5, 7, 9

Even numbers = 2, 4, 6, 8, 10

Total numbers = 9

Odd numbers = 4

Even numbers = 5

Now,

`P(odd)=(4)/(9)`

`P(Even)=(5)/(9)`

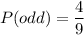
Expected value is

`E(x)=\sum x* P(x)`

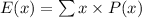
Player wins 1 dollar if the number on the ball is odd and loses 1 dollar if the number is even.

`E(x)=1* P(odd)+(-1)* P(even)`

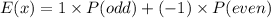
On substituting the values, we get

`E(x)=1* (4)/(9)+(-1)* (5)/(9)`

`E(x)=(4)/(9)-(5)/(9)`

`E(x)=-(1)/(9)`

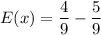
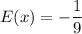
Therefore, the expected value of his winnings is
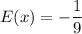`E(x)=-(1)/(9)`.