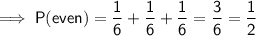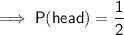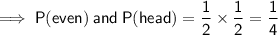Answer:
a) No, it does not matter whether you roll the die or flip the coin first, as these two events are independent of each other, which means they do not affect each other.
b) Yes.
- Let event 1 be flipping a coin and event 2 be rolling a die.
- Let event 1 be rolling a die and event 2 be flipping a coin.
The likelihood that any outcome will occur will not change, as the events are independent.
c) see attached
d) 12 outcomes (H = head, T = tail, numbers represent the value of the die)
H 1 T 1
H 2 T 2
H 3 T 3
H 4 T 4
H 5 T 5
H 6 T 6
e)