Answer:
Point-slope form:
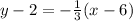
Slope-intercept form:
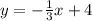
Explanation:
So, first, we need point-slope form.
Point-slope form:

In this form, m is your slope and
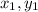 is your point.
is your point.
We have two points, so let's find the slope.
Slope formula:
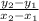
The y_2 and y_1 points can be interchanged, but order can't be changed (a y_2 can't go with an x_2).
For this problem, (-9,7) is going to be the x_2, y_2 pair.
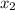 = -9
= -9
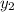 = 7
= 7
 = 6
= 6
 = 2
= 2
Let's put the values into the formula.
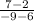 =
=
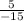 =
=
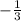
The slope is 1/3. Going back to point-slope form, let's put the slope in.

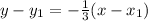
Now, lets put our x_1, y_1 point in.
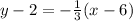
This is our point-slope form.
Now, to convert this to slope-intercept form, multiply everything out.
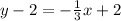
Add two.
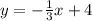
This is our slope-intercept form.
Hope this helped!