Question

Solve for x, 0 ≤ x ≤2π (2cosx-1)(2sinx+√3 ) = 0

Answer 1

x = π/3, x = 5π/3, x = 4π/3

Explanation:

Let's split the given equation (2cosx-1)(2sinx+√3 ) = 0 into two parts, and solve each separately. These parts would be 2cos(x) - 1 = 0, and 2sin(x) + √3 = 0.

`2\cos \left(x\right)-1=0,\\2\cos \left(x\right)=1,\\\cos \left(x\right)=(1)/(2)`

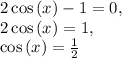
Remember that the general solutions for cos(x) = 1/2 are x = π/3 + 2πn and x = 5π/3 + 2πn. In this case we are given the interval 0 ≤ x ≤2π, and therefore x = π/3, and x = 5π/3.

Similarly:

`\:2\sin \left(x\right)+√(3)=0,\\2\sin \left(x\right)=-√(3),\\\sin \left(x\right)=-(√(3))/(2)`

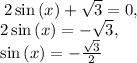
The general solutions for sin(x) = - √3/2 are x = 4π/3 + 2πn and x = 5π/3 + 2πn. Therefore x = 4π/3 and x = 5π/3 in this case.

So we have x = π/3, x = 5π/3, and x = 4π/3 as our solutions.