Question

5

Type the correct answer in each box.
Functions hand k are inverse functions, and both are defined for all real numbers.
Using this relationship, what is the value of each function composition?
(h o k)(3)=
(K o h)(-46)=

Answer 1

(h o k)(3)= 3

(K o h)(-4b)= - 4b

Explanation:

Composition of a function and its inverse function returns the input

(h o k)(3)= 3

(K o h)(-4b)= - 4b

Answer 2

`(h\circ k)(3)=3`

`(k\circ h)(-4b)=-4b`

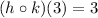
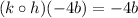
Explanation:

Remember that for two functions to be inverses, the following must be true:

`h(k(x))=k(h(x))=x`

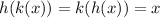
Since we know they are indeed inverses, they are true.

So, whatever input we put in, we'll just get it back out again.

So, for our first problem:

`(h\circ k)(3)`

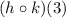
We can rewrite this as:

`=h(k(3))`

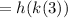
We can imagine our x being 3 here.

Therefore, using the above identity, we can conclude that:

`h(k(3))=3`

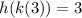
For our second example, the same thing:

`(k\circ h)(-4b)`

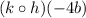
This is the same as saying:

`k(h(-4b))`

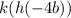
Again, using the above property, we can imagine our x is -4b. So, this will be equivalent to:

`k(h(-4b))=-4b`

And we're done!