Question

Find the standard form of the equation for the circle with the following properties.

Center (−6,−7/6) and tangent to the x-axis

Answer 1

`(x+6)^2+(y+(7)/(6))^2=(49)/(36)`

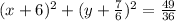
Explanation:

So, we know that the center of the circle is at (-6, -7/6).

To find the equation of our circle that is tangent to the x-axis, we just need to find the vertical distance from our center to the x-axis.

Our center is at (-6, -7/6). The vertical distance from this to the x-axis directly above will be (-6, 0).

So, find our distance by subtracting our x-values:

`d=r=0-(-7/6)`

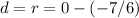
Subtract:

`d=r=7/6`

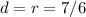
So, our distance, which is also our radius, will be 7/6.

Now, we can use the standard form for a circle, which is:

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the center and r is the radius.

Substitute -6 for h, -7/6 for k, and 7/6 for r. This yields:

`(x+6)^2+(y+(7)/(6))^2=(49)/(36)`

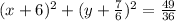
We can confirm by graphing (using a calculator):