Question

Company earns S dollars by selling y items per week. According to the equation S(y)=−2y^2+60y+10, how many items does company need to sell to maximize earnings.

Answer 1

`Max = 15`

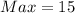
Explanation:

Given

`s(y) = -2y^2 + 60y + 10`

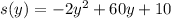
Required

Determine number of items that gives maximum earnings;

The general form of a quadratic equation is:

`s(y) = ay^2 + by + c`

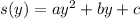
And the maximum is calculated as:

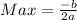`Max = (-b)/(2a)` If a<0

Comparing
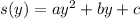`s(y) = ay^2 + by + c` to
`s(y) = -2y^2 + 60y + 10`

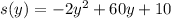
We have that:

`a = -2`
`b = 60`
`c = 10`

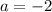
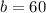
Substitute these values to

`Max = (-b)/(2a)`

`Max = (-60)/(2 * -2)`

`Max = (-60)/(-4)`

`Max = 15`

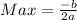
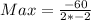
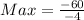
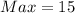
The number of item that maximizes the function is when y = 15