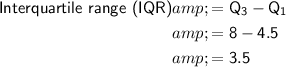Answer:
IQR = 3.5
Explanation:
Explanation of the given box plot:
- The closed circles at either end are the minimum and maximum
- The middle vertical line of the box is the median
- The left side of the box is the first quartile
- The right side of the box is the third quartile
Therefore, the Five-number summary of the given box plot is:
- Minimum = 3
- First quartile (Q₁) = 4.5
- Median (Q₂) = 6
- Third quartile (Q₃) = 8
- Maximum = 13