Question

Two identical stones are simultaneously launched horizontally from two slingshots at

the same height. Stone A is launched with an initial speed of 5 m/s. Stone B is
launched with an initial speed of 1 m/s. Which stone hits the ground first, and where
do they land?)

Answer 1

a) Both stones hit at the same time, b) Stones A and B will land at a distance of
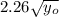`2.26\sqrt{y_(o)}` and
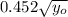`0.452\sqrt{y_(o)}` meters, respectively.

Step-by-step explanation:

Each stone experiments a parabolic motion, that is, the combination of a horizontal motion at constant velocity and a vertical uniform accelerated motion due to gravity. We know that each stone is launched horizontally at the same height and from the same initial position.

The equations of motion for each stone are described below:

Stone A

`x_(A) = x_(o) + v_(A,o)\cdot t_(A)`

`0 = y_(o) + (1)/(2)\cdot g\cdot t_(A)^(2)`

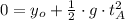
Stone B

`x_(B) = x_(o) + v_(B,o)\cdot t_(B)`

`0 = y_(o) + (1)/(2)\cdot g\cdot t_(B)^(2)`

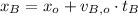
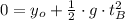
a) Which stone hits the ground first?

The stone that hits the ground first has the lowest time. If we know that
`v_(A,o) = 5\,(m)/(s)`,
`v_(B,o) = 1\,(m)/(s)`,
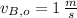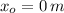`x_(o) = 0\,m` and
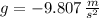`g = -9.807\,(m)/(s^(2))`, then the equations of motion are reduced into this:

Stone A

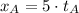`x_(A) = 5\cdot t_(A)` (Eq. 1)

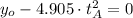`y_(o) -4.905\cdot t_(A)^(2)= 0` (Eq. 2)

Stone B

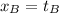`x_(B) = t_(B)` (Eq. 3)

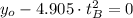`y_(o) -4.905\cdot t_(B)^(2)= 0` (Eq. 4)

From (Eq. 2) and (Eq. 4), we get that
`t_(A) = t_(B)`.

Both stones hit at the same time.

b) Where do they land?

From (Eq. 2) and (Eq. 4), we get:

`y_(o) = 4.905\cdot t^(2)`

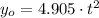
The time is cleared within the expression:

`t =\sqrt{(y_(o))/(4.905) }`

`t \approx 0.452\sqrt{y_(o)}`

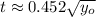
And from (Eq. 1) and (Eq. 3), we get the following equations of motion:

`x_(A)= 5\cdot t`

`x_(B) = t`

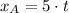
The horizontal distance taken by each stone is calculated by direct substitution on each expression:

`x_(A) = 2.26\sqrt{y_(o)}\,m`

`x_(B) = 0.452\sqrt{y_(o)}\,m`

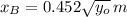
Stones A and B will land at a distance of
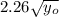`2.26\sqrt{y_(o)}` and
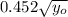`0.452\sqrt{y_(o)}` meters, respectively.