Question

AM= 2x+6, MB= 4x-2, and AB=22, By solving for X determine whether or not M is the midpoint of AB

Answer 1

M is not the midpoint of AB because AM does not equal MB.

Explanation:

AM+MB=AB, So (2x+6)+(4x-2)=22 when you plug in the numbers. So when you add like numbers for that equation you get 6x+4=22 subtract 4 from both sides you get

`6x + 4( - 4) = 22( - 4)`

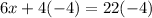
which then equals 6x=18. then you divide 6 by both sides to get x alone so its

`6x / 6 = 18 / 6`

and that equals x=3. now that you have what x equals you have to find AM and MB by plugging in x so,

AM=2(3)+6=12 then MB=4(3)-2=10. So because AM equals 12 and MB equals 10 AM does not equal MB so M is not the midpoint of AB because it doesnt divide both sides equally. :)