Answer:
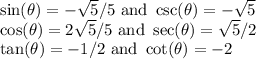
Explanation:
First, let's determine which quadrant our angle θ lies in.
Remember ASTC, where:
Everything is positive in QI,
Only sine (and cosecant) is positive in QII,
Only tangent (and cotangent) is positive in QIII,
And only cosine (and secant) is positive in QIV.
Since our tangent is negative, and our cosine is positive, this means that our θ must be in QIV.
In QIV, sine is negative, tangent is negative, and cosine is positive.
With that, let's figure out the remaining trig ratios.
We know that:
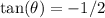
Remember that tangent is the ratio of the opposite side to the adjacent side.
Let's figure out our hypotenuse using the Pythagorean Theorem:

Substitute 1 for a and 2 for b (we can ignore the negative since we're squaring anyways). This yields:
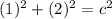
Square:
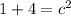
Add:
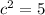
Take the square root:

So, our square root is √5.
So, our three sides are: Opposite=1, Adjacent=2, and Hypotenuse=√5.
Sine and Cosecant:
Remember that:
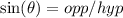
Substitute 1 for the opposite and √5 for the hypotenuse. This yields:
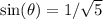
Rationalize:
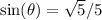
And since our angle is in QIV, we add a negative:
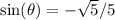
Cosecant is simply the reciprocal of sine. So:
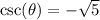
Cosine and Secant:
Remember that:

Substitute 2 for the adjacent and √5 for the hypotenuse. This yields:

Rationalize:
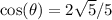
Since our angle is in QIV, cosine stays positive.
Secant is the reciprocal of cosine. So:

Tangent and Cotangent:
We were given that:
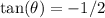
To find cotangent, flip:

And we're done!